Subtracting Radicals is Easy when you know how!

When subtracting radicals the steps involved are essentially the same as those involved in adding radicals, and  should only be attempted once simplifying radicals is fully understood.  

Your child should also know the rules for radicals and have had a chance to practice applying these rules.  Your student also has to be comfortable identifying perfect squares and perfect cubes, the skill required when simplifying radicals.

The Golden Rule of Subtracting Radicals
Only 'Like' Radicals can be subtracted!

Remember this rule when adding and/or subtracting, and you can't go wrong!

Only 'Like' radicals can be added or subtracted!  When you are presented with a problem, simply reduce each radical to its lowest form

and then operate (ie. add or subtract) as indicated.  Just like you did when you learned how to add and subtract fractions!  Only like with like!

Follow along with this worked example to see how we add these two radical numbers.

Example

Steps to Subtract

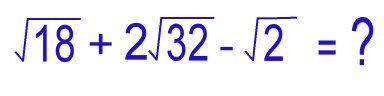Confirm you are subtracting like terms (identical radicals). We DO NOT have Identical radicals, so we must simplify them so we can move forward.

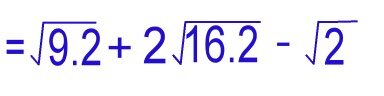We can see that 18 = 9 x 2 (where 9 is equal to the perfect square of 3) - we apply rule 1 of radicals. We can see that 32 = 16 x 2 (where 16 is equal to the perfect square of 4) - we apply rule 1 of radicals.

We apply rule 1 of radicals again, to find the root of the perfect square and bring it outside the radical .

Root(ab) = root a x root b

Now we simply 'tidy things up'.

We have now simplified the radicals so they are all "alike" Now we operate as indicated. 3 + 8 - 1 = 10 We have now completed the problem

SOLUTION

As you can see from this worked example - the skill to subtracting radicals, is not the subtraction process, but the process of identifying perfect squares or perfect cubes and being able to simplify the radical to its lowest terms.  Once your child has successfully completed a number of these adding and subtracting radical numbers they will never make them anxious again.

More information in our Algebra Section

Radicals

Exponents

  • What are Exponents
  • Perfect Square
  • Perfect Cube
  • How to label 
  • Exponents with negative base
  • Operating on exponents

Monomials

Properties of Arithmatic

Polynomials

  • Polynomials
  • Labeling Polynomials
  • Adding and Subtracting
  • Multiplying and Dividing

Keep In Touch!

You can send me a quick message, follow me on Facebook  or why not join our community of like minded parents? Choose all the options so you don't miss any of the new material added to this site.