Adding Radicals is Easy when you know how!

Adding Radicals should only be attempted once simplifying radicals is fully understood.  Your kid should also know the rules for radicals and have had a chance to practice applying these rules.  

Your student also has to be comfortable identifying perfect squares and perfect cubes,the skill required when simplifying radicals.

The Golden Rule of Adding Radicals

Only 'Like' Radicals can be added.

Remember this rule when adding, and you can't go wrong!

Only 'Like' radicals can be added!  

So what were they thinking when they gave you a question, such as:

It can't be done!  Right? .... Wrong!  It can be done - and what they were thinking was - "let the games begin!"

And this is something your student must now get used to!  Algebra is a game.  It is simply about manipulating numbers (while ALWAYS obeying the rules) to make them do what YOU want them to do!

Follow along with this worked example to to watch the mathematical magic unfold and see how we add these two radical numbers.
  1. Confirm you are adding like terms (identical radicals)

We DO NOT have Identical radicals, so we must simplify them so we can move forward.

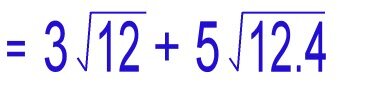We can see that 48 = 12 x 4 (where 4 is equal to the perfect square of 2) - we apply Rule 1 of radicals.

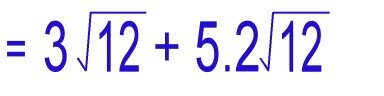We apply Rule 1 of radicals again, to find the root of the perfect square and bring it outside the radical.

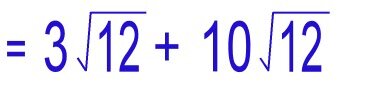We could now add these two radical numbers to get an answer of 13Root12.

But we see that 12 is also composed of the products of 4 and 3; 4 again being the result of the perfect square 2, so we are not finished yet!

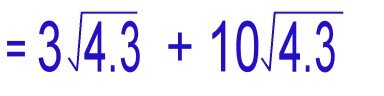We apply Rule 1 of radicals again this time to BOTH numbers.

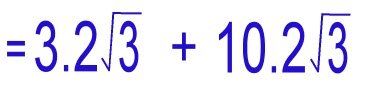We now tidy up everything, before we add to ensure no errors.

  • (3x2)root3 = 6root3
  • (10x2)root3 = 20root3

We are NOW adding 'Like' radicals

6 + 20 = 26

6root3 + 20root3 = 26root3

Does adding Radicals always take so many steps?

No - it is all about familiarity and confidence with regards to 'seeing' the factors of the root and knowing perfect squares and cubes.

Had we taken a little more time looking at these root, we could have noticed that:

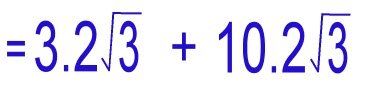  • 3 and 4 are factors of 12, where 4 is a perfect square and
  • 3 and 16 are factors of 48, where 16 is a perfect square

Had we been more aware of our Perfect Squares and Factors, we could have gotten to this stage in one move!

As you can see from this worked example - the skill to adding radicals, is not the addition process, but the process of identifying perfect squares or perfect cubes, knowing how to factorize numbers and knowing the Rules of Radicals to simplify the radical to its lowest terms.  

Once your child has successfully completed a number of these problems, adding and subtracting radical numbers will never again make them anxious. 

If you enjoyed the information presented here on the topic of adding radicals, please continue to explore all the Basic Algebra section.

Printable Math Worksheets offers so much more than math practice! Start discovering all of it.

Keep In Touch!

You can send me a quick message, follow me on Facebook  or why not join our community of like minded parents? Choose all the options so you don't miss any of the new material added to this site.