Dividing Radicals can seem overwhelming ....

...but all you need to know is...ONE Rule of Algebra to be successful EVERY TIME!

The trick is to simply get rid of the radical numbers in the denominator!  

When we do this, we say we rationalize the denominator.

Easier said than done - I hear you say!  Well it is actually quite easy to do and to show you how, I am going to take a step back to one of the basic Algebra Formula you should already be familiar with.

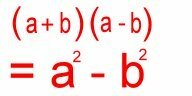
When this algebraic rule is applied to radicals you get:

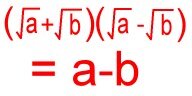
Remember this rule when dividing, and you can't go wrong! Follow along with this worked example to see how we divide these two radical numbers.

Dividing Radical Numbers - Worked Examples

Divide 2 by 3 - Root7

We have to eliminate the Root7 from the Denominator - rearrange the Denominator to contain TWO radicals.

   X = Root(X^2) so 3 = Root9

We now have the denominator in the for Root a - Root b.

Apply the Rule above!

We now have radical numbers in the numerator and only real numbers in the Denominator

We have to eliminate the Root7 from the Denominator

 (2Root9) over 2 = Root9 = 3

 (2Root7) over 2 = Root7

As you can see from this worked example - the skill to dividing radicals, is not the division process, but the process of identifying  the rules of algebra, and being able to apply them to radical numbers - and also, knowing the rules of radicals, and how to simplify them.

If you enjoyed the information presented here on the topic of dividing radicals, please explore all the other great information I offer in Basic Algebra. 

Don't forget that you can explore all of what Printable Math Worksheets has to offer from the home page.

Keep In Touch!

You can send me a quick message, subscribe to K6Math Fun & Update, or join my Facebook Page - K6Math. Choose all the options so you don't miss any of the new material added to this site.